Nov 1 2021
La scala dei suoni sacri
Armonizzazione di 432, 528, 424 e
440 Hz in un’unica sintonizzazione
Definizione numerica accurata
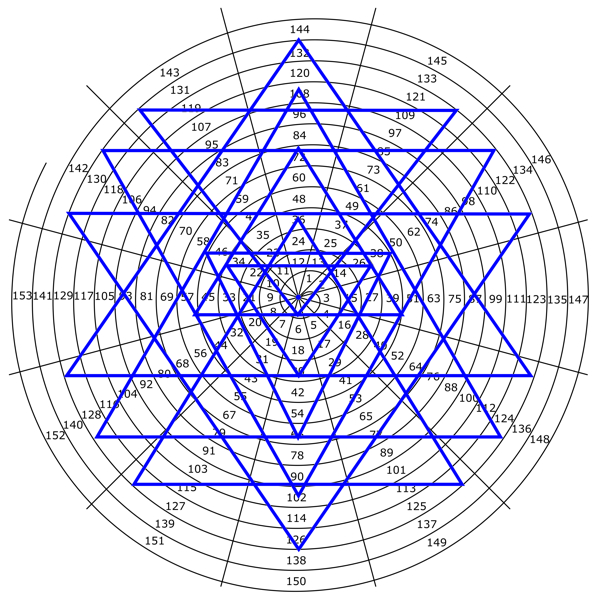
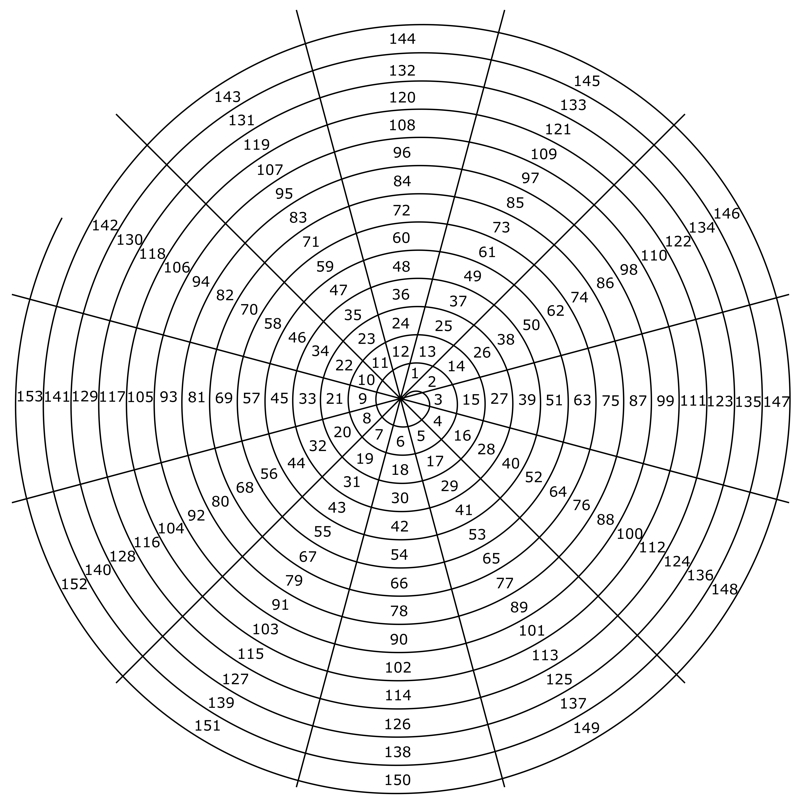
C’è una sintonizzazione in cui le frequenze 432, 528, 424 e 440 Hz possono coesistere pacificamente. La scala ha 32+1 toni armonici puri e la frequenza di riferimento di 256 Hz. Proviene dalla Serie Naturale Ascendente di Armoniche da 32 a 64 del Tono Fondamentale a 8 Hz, e rappresenta i suoi 6esimo doppio. Io chiamo questa accordatura La Scala dei Suoni Sacri.
Rappresentazione usando l’antica matematica sumera/babilonese/vedica:
32; 33; 34; 35; 36; 17 anni 18 anni 39; 40; 41; 42; 43; 44; 45; 46; 47; 48; 49; 50; 51; 52; 53; 54; 55; 56; 57; 58; 59; 60; 61; 62; 63; 64
Rappresentazione con rapporti
musicali: 1/1; 33/32; 17/16; 35/32; 9/8; 37/32; 19/16; 39/32; 5/4; 41/32; 21/16; 43/32; 11/8; 45/32; 23/16; 47/32; 3/2; 49/32; 25/16; 51/32; 13/8; 53/32; 27/16; 55/32; 7/4; 57/32; 29/16; 59/32; 15/8; 61/32; 31/16; 63/32; 2/1
La matematica per derivare una delle serie precedenti dall’altra è semplice. Dividi tutti i numeri della serie antica per il primo, quindi semplifica le frazioni. Al contrario, la serie di rapporti può essere trasformata nella serie di interi calcolando il loro minimo comune denominatore (il più piccolo numero intero che è un multiplo di tutti i numeri sotto la barra della frazione) e scartandolo.
Rappresentazione logaritmica con costanti musicali (definizione data più in basso):
0.000; 30,772; 60,625; 89,612; 117,783; 145,182; 171,850; 197,826; 223,144; 247,836; 271,934; 295,464; 318,454; 340,927; 362,905; 384,412; 405,465; 426,084; 446,287; 466,090; 485,508; 504,556; 523,248; 541,597; 559,616; 577,315; 594,707; 611,802; 628,609; 645,138; 661,398; 677,399; 693,147
Se 1/1 oscilla con una frequenza di 256 cicli al secondo, i valori
esatti dei toni espressi in Hertz sono: 256; 264; 272; 280; 288; 296; 304; 312; 320; 328; 336; 344; 352; 360; 368; 376; 384; 392; 400; 408; 416; 424; 432; 440; 448; 456; 464; 472; 480; 488; 496; 504; 512[; 528; 544; 560; …]
È così che vengono calcolate le frequenze di cui sopra: ogni rapporto musicale (o il suo risultato) viene moltiplicato per 256. Oppure, ogni numero intero dell’insieme antico viene moltiplicato per 8, perché tutte le figure nell’insieme sono le armoniche ascendenti (chiamate anche armoniche) da 32 a 64 del tono fondamentale a 8 Hz. In realtà, è da qui che proviene la frequenza di riferimento 256 Hz: è il 32nd armonica del Tono Fondamentale 8 Hz (32 x 8 = 256).
528 non appare direttamente all’interno del doppio centrale, ma la sua metà – 264 Hz – sì. Ciò significa che 528 è il secondo tono del doppio successivo, che continua la progressione di cui sopra con 528; 544; 560; … e così via Hz. 512 ha il ruolo dell’ultimo (33rd) frequenza nel doppio centrale e quella del primo nel successivo.
Scala dei suoni sacri come armoniche antiche (numeri esterni)
e alcuni valori in Hertz per il tono fondamentale 8Hz (numeri interni)
La terminologia giusta
Si noti quanto sia inappropriato il termine “ottava” – che significa “l’8esimo nota” – è qui. Anche nella teoria musicale moderna, il 13esimo “nota” è ancora chiamato “ottava” nonostante il fatto che il sistema a 7 toni sia stato ampliato per centinaia di anni a 12. Un approccio corretto alla Scala dei Suoni Sacri sarebbe quello di usare in qualche modo il numero 33 nel nome, perché questo è il 33rd tono, ma per semplicità uso il termine “doppio”. Questo descrive perfettamente il fenomeno acustico del raddoppio della frequenza che avviene man mano che la serie progredisce e corrisponde accuratamente a qualsiasi altra scala di qualsiasi numero di toni.
La moderna teoria musicale occidentale considera qualsiasi tono la cui frequenza è stata dimezzata o raddoppiata per rappresentare lo stesso suono. I musicisti usano lo stesso nome anche per toni che sono uno o più doppi a parte, anche se non sono lo stesso tono. Raddoppiare o dimezzare la frequenza di un tono non restituisce lo stesso tono, perché x ≠ 2x ≠ x/2. Questa è una semplice convenzione, che non ha assolutamente alcuna base naturale, nessuna base fondamentale. Se dovessi raddoppiare le vibrazioni atomiche di un gatto, con qualche processo misterioso, non sarà più lo stesso gatto, e probabilmente non più un essere vivente. Se prendi un suono e alzi il suo tono, non è più lo stesso suono.1
Nel caso ve lo stiate chiedendo, 424 Hz è la “Frequenza Standard di Madre Natura”, o lo standard di sintonizzazione “RA Music”. Dai un’occhiata a ramusic.com per maggiori informazioni.
Il nome Sacred Sounds Scale non implica che certe frequenze misurate in Hertz come 424, 432, 440 o 528 siano sacre, ma che la scala stessa – o meglio ancora, la Serie Naturale di Armoniche Ascendenti (overtones) da cui deriva la scala – sia sacra. Questo perché la Serie Armonica viene dalla Natura; non è un prodotto della cultura o dell’intelletto umano. A questo proposito, la Serie Armonica Naturale è pre-umana; è stato parte dell’Universo per tutto il tempo in cui l’Universo è esistito. Non c’è niente di più naturale, più consonante e in sintonia con se stessa della Serie Armonica.2
Armoniche di un tono fondamentale
Frequenze come 528, 432 e 424 sono state chiamate “Universali”, “Cosmiche”, “Sacre”, “Naturali” e “Curative”; questo perché, insieme a 440, sono tutte armoniche del Tono Fondamentale a 8 Hz. Sebbene al di sotto della gamma uditiva umana, la frequenza estremamente bassa (ELF) di 8 Hz fa parte della gamma di frequenze delle onde cerebrali alfa ed è uno dei picchi di spettro del nostro impulso terrestre chiamato risonanza di Schumann, che negli ultimi decenni ha segnato in media circa 7,83 Hz. Uno studio condotto presso la Society for Scientific Exploration (SSE) ha esplorato i modelli EEG di guarigione energetica, misurando sia il guaritore che il soggetto, concludendo che questa onda stazionaria terrestre sempre presente che varia vicino a 8 Hertz potrebbe essere un meccanismo per la guarigione a distanza.3
Variabilità della risonanza di Schumann misurata in Antartide.4
8 Hz è anche estremamente vicino alla frequenza primaria della matrice del mereone: 7,97 Hz e, secondo il mereon Legacy CIC Research Team, questa è la stessa frequenza emessa dai delfini.5 Template Architects Juliet e Jiva Carter hanno motivo di credere che 8 Hz sia la frequenza dell’ex pianeta Maldek, che ora chiamiamo “la fascia degli asteroidi”.6 C’è la possibilità che questo pianeta, in una corretta interpretazione delle prove storiche soppresse, fosse la casa di un continente perduto che tutti conosciamo…
Cosa significa veramente “Tuning”
La frequenza 444 Hz non fa parte della Sacred Sounds Scale perché è solo una controparte approssimata di 528 da un altro sistema di sintonizzazione. Quando 528 è integrato nella scala temperata uguale di 12 toni artificiali, è il primo tono. Convenzionalmente, tuttavia, non è l’1san frequenza che è presa come riferimento, ma il 10esimo. Questo è ovviamente arbitrario, ma è la procedura standard. Ecco perché i musicisti non dicono mai “sintonizzati su 261,625565300599…”; dicono semplicemente “tune to 440”.
La matematica utilizzata per calcolare il 10esimo passo equivalente di 528 Hz non è sole, perché il temperamento uguale si basa sul 12esimo radice di 2, cioè ¹²√2 o 2^(1/12). La serie di numeri risultante ha decimali non ricorrenti e infiniti; questi numeri non possono essere trovati in natura, anche se sono in ogni canzone che abbiamo mai sentito in Occidente (esistono delle eccezioni). Quindi il 10esimo il passo sarebbe 528 × 2^(9/12) = 887,986614507922… che diviso per 2 restituisce 443,993307253961… Hz – quasi 444. In questo modo, i musicisti che usano lo standard comune diranno “tune to 444” e con questo in realtà intendono “tune to 528” in uguale temperamento.
Si noti l’inevitabile ambiguità della nomenclatura: il termine “accordatura” è usato sia per “scala di tono”, sia per la “frequenza di riferimento” di quella scala.
- Una “scala tonale” è una scala astratta di suoni, un insieme di numeri correlati che definiscono le singole entità di un sistema e la loro relazione con il primo membro della serie. In tutte le culture del mondo, è l’accordatura della scala – o relazione matematica tra i toni – che gioca il ruolo chiave nell’identità musicale.
- La “frequenza di riferimento”, detta anche “frequenza standard” e “intonazione da concerto” è un aspetto secondario dell’accordatura, attraverso il quale il primo membro della scala, l’1/1, viene assegnato ad una specifica frequenza espressa in Hertz. I toni rimanenti della scala, essendo matematicamente correlati al primo, lo seguiranno cambiando frequenza di conseguenza.
Storicamente, la frequenza di riferimento della scala a 12 toni è definita dal 10esimo tono invece di 1san. Ciò significa un ulteriore passo nel calcolo della vera frequenza di riferimento su 1/1. Prendiamo come esempio il pitch del concerto a 432 Hz. Per trovare la frequenza di riferimento corretta di 1/1, dobbiamo prima informarci sul tipo della nostra scala a 12 toni. Sappiamo che 432 è il 10esimo tono, ma di che tipo di accordatura in scala stiamo parlando: “Pitagorico”, Just Intonation, temperamento uguale, Serie armoniche, uno dei miriadi di Momenti di simmetria (MOS), o qualsiasi altra alternativa?
Questo è estremamente importante, perché se 432 è un “pitagorico” 27/16, allora 1/1 = 432 ÷ 27/16 = 256 Hz; se si tratta di una Just Intonation 8/5, allora 1/1 = 432 ÷ 8/5 = 270 Hz; se è uguale temperato, allora 1/1 = 432 ÷ 2^(9/12) = 256,868736840587… Hz, e così via: un valore diverso per ogni scala.
Questo complica anche il problema 528, perché questa frequenza è dall’inizio l’1/1 della scala, e trovando il suo 10esimo Tono equivalente solo per amore del conformismo ci getta di nuovo nel regno delle scale: a quale scala dovremmo sintonizzarci? Se è “pitagorico”, la risposta è 528 × 27/16 ÷ 2 = 445,5 Hz; se si tratta di Just Intonation, la risposta è 528 × 8/5 ÷ 2 = 422,4 Hz; se è uguale temperamento, la risposta è 443,993307253961… Hz come calcolato sopra, e così via: un valore diverso per ogni scala.
Riesci a capire l’1/1 della frequenza di riferimento di 424 Hz per la “Pitagora”, Just Intonation e le scale temperate uguali?
Nella vita di tutti i giorni e nella pratica musicale moderna, tuttavia, scale diverse sono di default fuori questione. C’è solo una scala in uso, ed è implicita come standard: la scala temperata uguale. Ogni volta che ci troviamo di fronte all’accordatura di uno strumento musicale – sia acustico che digitale – a una frequenza di riferimento, la scala utilizzata è il temperamento dissonante e stonato uguale. Questo perché il temperamento uguale è stato per così tanto tempo parte della nostra cultura, che la sua validità non è più messa in discussione. Inoltre, gli strumenti acustici come le chitarre non hanno modo di cambiare scala – sono bloccati in un temperamento uguale. Possono cambiare la frequenza di riferimento, ma questo non aiuta molto. L’unica soluzione è quella di refret (vedi “Strumenti musicali” sotto), o rimuovere completamente i tasti.
Alvarez MC90 Fretless Conversion Primo piano della tastiera7
Nell’accordatura della Scala dei Suoni Sacri, tutti i problemi di cui sopra sono elegantemente affrontati dalla natura stessa della scala, che è armonicamente pura e progredisce naturalmente, e assegnando la frequenza di riferimento al primo tono della scala: 1/1. Questo è in conformità con le Leggi Universali del Suono. Vale la pena ricordare qui che, contrariamente alla credenza popolare, il tono chiamato “A” non è il primo nel sistema a 12 toni, né lo è “C” per quella materia. Storicamente, e anche qui siamo di fronte a convenzioni arbitrarie, il primo tono della scala, l’1/1, è “D”.
Denominazione dei toni
Questo ci porta al delicato argomento del dare un nome ai toni. Sarebbe inutile provare ad adattare i vecchi nomi a questa nuova (ma in realtà vecchia come l’Universo), principalmente perché i due sistemi sono molto diversi. Il temperamento standard a 12 toni uguali è un’approssimazione ciclica di una scala a spirale fatta esclusivamente dall’impilamento dell’intervallo tra i 2nd e 3rd armoniche su se stesso, dividendo liberamente i valori di tono per 2, la cui configurazione iniziale di soli 7 toni ha originato i nomi che abbiamo conosciuto come C D E o Do Re Mi, insieme ai loro taglienti e piatti controintuitivi.
Al contrario, la Sacred Sounds Scale è accordata in modo non lineare secondo la Natural Harmonic Series e questo la rende incompatibile con la scala standard a 12 toni – sia matematicamente che “alfabeticamente”. Se finora ho presentato l’accordatura della scala dei suoni sacri come un fatto, un evento naturale pre-umano, i seguenti nomi di tono sono solo un’idea che sembra funzionare:
I toni 32+1 della Scala dei Suoni Sacri potevano portare nomi di lettere. L’alfabeto “latino” o “romano” contiene solo 26 lettere, senza contare i segni diacritici. I primi 8 di questi, da A a G più H, sono già stati utilizzati per il sistema a 12 toni, quindi per evitare confusione saranno trascurati. Questo ci lascia con 18 lettere, di cui W richiede troppo tempo per pronunciare nella maggior parte delle lingue, quindi siamo scesi a 17. Se dovessimo nominare solo ogni altro tono della Scala dei Suoni Sacri, il primo sarebbe İ, la terza J, la quinta K e così via, terminando la serie con Z e lasciando metà della scala senza nome. Questi toni senza nome potrebbero portare i nomi dei toni di fronte a
loro con un segno “+” aggiunto, quindi: İ; İ+; J; J+; K; K+; L; L+; M; M+; N; N+; O; O+; P; P+; Q; Q+; R; R+; S; S+; T; T+; U; U+; V; V+; X; X+; Y; Y+; Z
Non c’è meno, perché questa è la Serie Ascendente di Armoniche. È una progressione sempre crescente di intervalli musicali disuguali e naturali. Tutti i toni contrassegnati con il segno più sono nuovi nel 6esimo doppio. Con altre parole, il 5esimo il doppio del Tono Fondamentale a 8 Hz contiene tutte le armoniche da 16 a 32, rappresentate dalle lettere da İ a Z senza alcun segno aggiuntivo aggiunto, e le 6esimo raddoppia le dimensioni aggiungendo un tono in più tra tutti gli altri per completare le armoniche da 32 a 64. Queste sono tutte le lettere da İ a Z contrassegnate con “+”.
La scelta di fare di “İ” il primo tono o 1/1 della scala non è arbitraria e dà alla scala significato e identità. Questa lettera di una parola è presa come la definizione di “me” nella lingua inglese; è la fonte da cui tutti gli altri toni traggono la loro individualità. Provengono tutti da, e fanno tutti parte della “İ” della scala.
Sebbene non sia lo stesso con la “notazione scientifica del tono” – un metodo di denominazione lettera-numero ideato per la scala cromatica occidentale standard (temperamento uguale a 12 toni) – i nomi delle lettere della scala della serie armonica da 16 a 32 portano numeri pedice per identificare il doppio del tono in modo simile. Nel nostro sistema, İ0 ha esattamente 16 Hz , un valore intorno alla fascia bassa della gamma uditiva umana. Si noti che Z0 suona lo stesso tono di İ1. Questo perché Z è l’ultimo tono musicale nella scala, e nel doppio successivo è il primo. Quindi, invece di avere due toni diversi che portano lo stesso nome (numeri esclusi, come nell’attuale pratica anti-musicale), abbiamo un tono che porta due nomi a seconda del contesto.
Questo sistema permette, per la prima volta nella storia della musica, di rappresentare accuratamente la Serie Armonica esattamente
com’è, facendo uso dei toni da essa derivati e dei rispettivi nomi: İ0; Z0(İ1); Q1; Z1(İ2); M2; Q2; U2; Z2(İ3); OKAY3; M3; O3; Q3; S3; U3; X3; Z3(İ4); J4; OKAY4; L4; M4; N4; O4; P4; Q4; R4; S4; T4; U4; V4; X4; Y4; Z4(İ5); İ+5; J5; J+5; OKAY5; K+5; L5; L+5; M5; M+5; N5; N+5; O5; O+5; P5; P+5; Q5; Q+5; R5; R+5; S5; S+5; T5; T+5; U5; U+5; V5; V+5; X5; X+5; Y5; Y+5; Z6
Strumenti Musicali
La Scala completa dei Suoni Sacri può essere mappata sulla Tastiera Terpstra,uno strumento musicale unico che può ospitare assolutamente qualsiasi accordatura – sia essa sotto forma di scale moderne, popolari, etniche, aborigene o storiche di 7, 8, 9, 12, 13, 16, 17, 18, 19, 22, 23, 26, 27, 29, 31, 32, 33, 37, 39, 40, 41, 42, 43, 45, 46, 47, 49, 50, 52, 53, 55 e 56 toni, e numeri ancora più grandi come 67 e 74 attraverso il principio della modularità. Naturalmente una scala con uno qualsiasi dei numeri di toni menzionati può essere sintonizzata in più modi e su qualsiasi frequenza di riferimento; inoltre, qualsiasi accordatura immaginabile di qualsiasi numero di toni può essere mappata sul layout di Terpstra.
Mappatura della tastiera
Terpstra alla serie naturale ascendente di armoniche da 32 a 64
I toni che raddoppiano/dimisono la loro frequenza sono sempre sullo stesso asse orizzontale e alla stessa altezza chiave. Rispetto alle limitazioni del sistema a 12 toni, 32 è meglio – 8/3 volte meglio. Immagina un pittore che deve dipingere con soli 12 colori, o un poeta che deve scrivere con una quantità limitata di parole… 32 porta nuove sfumature, sottigliezze e può esprimere meglio artisticamente la complessità delle esperienze umane e la ricerca del Divino.
AGGIORNAMENTO. Riproduci la serie naturale ascendente di armoniche da 32 a
64 (scala dei suoni sacri) online: Terpstra Keyboard WebApp | 32-JI-61L Sacred Sounds Scale — arcaica ratios notation
Terpstra Keyboard WebApp | 32-JI-61L Sacred Sounds Scale — notazione delle frazioni musicali
La parte migliore della terpstra Keyboard, oltre al suo meccanismo magnetico di rilevamento dei tasti che lo rende uno dei controller più espressivi mai costruiti (ogni tasto è un piccolo controller continuo), e il fatto che ogni tasto può cambiare colore in base alla sintonizzazione, è l’isomorfismo. Ciò significa che, a differenza della tastiera per pianoforte standard 7-white/5-black che è un incidente storico con layout irregolare, il Terpstra è regolare e richiede solo una posizione del dito per ogni tipo di accordo, indipendentemente da dove si trovano le dita sul keybed.
Tastiera Terpstra (1san Gen.) – 280 controllori continui che cambiano colore8
Un’altra alternativa alla tastiera standard irregolare è la “Nuova tastiera” ideata da Johannes Kotschy, che è stata appositamente progettata per la serie Armonica o Naturetone-System, come la chiama il suo inventore.9 Su questo strumento, che non è mai stato costruito, i 32 toni della Scala dei Suoni Sacri cadono naturalmente, mentre i toni effettivi sono creati dalla stessa disposizione dei tasti attraverso l’aggiunta di toni selezionati. L’idea di un sistema di accordatura basato su Armoniche Naturali non è nuova ed è stata proposta – tra gli altri – anche da Sergio Aschero (che chiama una delle sue forme estese “Afinación Armónica base 64” che significa “accordatura armonica in base 64”10) e Johnny Reinhard (nella sua forma massimizzata di 128 toni: “128 tuning”11).
L’idea della nuova tastiera12
Strumenti elettronici in grado di liberare la musica dalla tirannia dell’uguale temperamento sono disponibili dal 1919, con l’invenzione del theremin o ætherphone: uno strumento musicale che veniva (ed è tuttora) suonato senza toccarlo13. Sfortunatamente, la maggior parte se non tutte le esibizioni di theremin fanno un uso esagerato del vibrato, una tecnica generalmente utilizzata per mascherare le brutte percosse di accordi temperati uguali che accompagnano gli artisti. Come tale, la musica theremin suona inquietante ed è stata estremamente utilizzata per i film horror. Mi piacerebbe sentire questo strumento suonato correttamente, senza la “mano tremante” responsabile della sua scomoda reputazione, e prodotto attraverso un modulo di sintesi sonora avanzato che arricchirebbe le sue capacità sonore.
Altri strumenti elettronici realmente in grado di controllare il passo continuo sono la tannerina e l’ondes martenot. Entrambi hanno il classico layout irregolare del pianoforte come riferimento, per tenerti in qualche modo bloccato nel credere che il modello 7-bianco / 5-nero sia musicalmente rilevante quando è vero l’esatto opposto. Una volta scartato questo, la libertà di pitch già disponibile nelle tue mani assume un significato completamente nuovo. Questo vale anche per il trautonio, che può funzionare senza che le leve fisse ne limitino il continuum di passo.
Le chitarre acustiche possono essere agitate o refretted per suonare la serie armonica da 32 a 64 della Scala dei suoni sacri. Un buon esempio è la chitarra Harmonic Series di Dante Rosati, con una tastiera personalizzata codificata a colori (manico della chitarra).14 Tom Winspear ha sperimentato un layout di tastiera su una scala 34 pollici / 864 mm, basso acustico a 5 corde convertito in chitarra a doppia corda Harmonic Series, dove le corde aperte sono accordate precisamente su İ2−İ3 Q2−Q3 IO3−İ4 Q3−Q3 IO4−İ4.15 Se queste corde fossero accordate in modo diverso, il modello di tasti rifletterebbe il cambiamento di conseguenza.
 Harmonic Series Harmonic SeriesGuitar Neck di Dante Rosati16 |  Esperimento Esperimentodi tastiera di Tom Winspear su un basso acustico a 5 corde convertito in chitarra della serie armonica17 |  Strumento costruito dal liutaio Walter Vogt che utilizza il suo sistema Mobile Fret18 Strumento costruito dal liutaio Walter Vogt che utilizza il suo sistema Mobile Fret18 |
Il modo più semplice per sperimentare diversi layout di tasti per chitarre, e allo stesso tempo mantenere la versatilità al massimo, è quello di utilizzare un sistema di tasti mobili regolabile á la Walter J. Vogt.19 La configurazione visualizzata (nell’immagine a destra) sopra ha l’accordatura İ; J+; M; N; Q+; 105/64; U; Z, dove 105/64 sta per Armonica 105 della Serie Ascendente da 64 a 128, che è un tono armonico puro di occorrenza naturale tra S e S +. L’1/1 della scala ha una frequenza di 268,190476… Hz (schema ripetuto dei decimali), calcolato per il tono 105/64 su 440 Hz.20 Un altro modo di avere più accordature su uno strumento a tono fisso come la chitarra fretted sono le tastiere intercambiabili, o centralni, come li chiama il loro inventore Tom Stone.21
La chitarra
Switchboard di John Schneider insieme a varie tastiere che ha costruito per essa22
Flauti, sax, insieme a tutti gli altri strumenti della famiglia wind & reed che usano i fori delle dita per cambiare tono oltre all’overblowing, possono essere suonati in quasi tutte le accordature con l’uso di diverse tecniche che si basano sul virtuosismo del giocatore, ma possono anche essere sintonizzati con precisione sulla serie armonica annoiando i fori di conseguenza. In effetti, oserei dire che qualsiasi strumento musicale potrebbe essere adattato per suonare almeno una parte di questa scala.
Ad esempio, la famiglia di strumenti in ottone valvolato deriva le loro altezze dalla serie di overtone [armonici] di diverse lunghezze di tubo. Accordando queste lunghezze in proporzioni razionali l’una con l’altra attraverso diverse riconfigurazioni valvolari, la serie overtone diventa prontamente disponibile su corni, tuba e tromboni [valvolati].23 Naturalmente il trombone ha già un controllo continuo del tono in modo che possa naturalmente suonare tiri senza restrizioni, proprio come il fischietto e il bottaio – uno strumento a fiato slide unico che Jacob A. Barton ha contribuito a inventare nel 2005.24 Johnny Reinhard è noto per aver suonato il fagotto nella scala naturale a 128 toni della serie armonica, che è un’espansione della scala qui presentata che include tutti i suoi toni.11 Poi ci sono l’alforo, il bucium, la trembita e l’erke, tutti strumenti di tipo labrofono in grado solo di produrre i tono della Natural Harmonic Series. E naturalmente il didgeridoo.
Non dimentichiamo gli strumenti esistenti che possono suonare qualsiasi scala (scala Harmonic Series inclusa) così come sono: violini, viole, violoncelli e tutti gli altri strumenti della famiglia delle corde ad arco come sarangi, goje, erhu e tutta la famiglia di strumenti huqin, morin khuur, kamança & kemençe e tutti della famiglia kamancheh, ravanahatha, k’ni, jawzah più tutti gli altri derivati dalla famiglia di strumenti rabāb ad arco; anche strumenti a pizzico come il basso fretless, guitarrón, chitarra lap steel hawaiana e il suo fratello maggiore il pedal steel, shamisen & sanshin, sanxian & shanz (shudraga), dan tam (ta in), sarod, doshpuluur & tobshuur, chitravina (gotuvadyam), komuz, kibangala (gabusi), ud & gambus & cobză con tutte le altre famiglie di strumenti oud, guqin (“lo strumento dei saggi”), sugudu & dramyen, dotara, insieme ad ogni altro strumento fretless delle famiglie di liuto pizzicato (o rubāb) e cetra, e l’elenco continua. È necessaria una ricerca approfondita per completare l’elenco.
Ma soprattutto, a causa della vera accordatura armonica della scala dei suoni sacri, questi sono tutti strumenti di guarigione. Ognuno di noi è una sinfonia, un grande concerto di frequenze che risuonano su scale diverse. Il nostro progetto divino di creazione giace dormiente dentro di noi, e noi siamo quelli che devono trovare la giusta frequenza per attivarlo. Ora abbiamo gli strumenti per farlo. Siamo i nostri guaritori del suono, purché stiamo lontani dalle accordature temperate.
Unità di misura
32 potrebbe sembrare molto, ma se prestiamo attenzione a tutte le canzoni che hanno mai toccato i nostri cuori noteremo che non importa il luogo e l’ora, solo 7 toni sono stati usati al massimo. Ci sono ovviamente delle eccezioni, ma in ogni cultura e in ogni periodo di tempo, il numero massimo di toni usati in una canzone era 7. La scala cinese a 5 toni, i 12 toni temperati della cultura occidentale, le classiche scale arabe a 17 e le scale indiane a 22 toni usano al massimo 7 toni in ogni data composizione. Quindi non c’è bisogno di andare per l’intera gamma 32. E se non ti piacciono i 440 Hz, toglilo dalla tua musica non usando il rapporto 55/32.
I valori in centesimi per i toni della Scala dei Suoni Sacri non sono stati dati, perché il centesimo è l’unità di misura logaritmica più inappropriata per gli intervalli musicali mai concepita. Il centesimo è stato introdotto circa 100 anni fa ed è ampiamente usato per nascondere la bruttezza dei numeri irrazionali artificiali che compongono lo stesso temperamento. Espresso in centesimi, il temperamento uguale a 12 toni sembra una progressione ordinatamente organizzata mentre qualsiasi altra accordatura sembrerà un pasticcio disordinato: dalle diverse versioni della sola intonazione alla serie armonica stessa. La maggior parte delle persone nuove alla teoria musicale non ha idea di cosa siano realmente questi centesimi; se lo facessero, molto probabilmente li considererebbero malvagi. Il centesimo è un insabbiamento della dissonanza: dà valori interi (o razionali) ai numeri irrazionali e fa sembrare innaturali i numeri armonici razionali.
Il calcolo dei centesimi fa uso del logaritmo di base 2, a causa della falsa concezione che qualsiasi tono la cui frequenza è moltiplicata o divisa per 2 è lo stesso tono. Per calcolare il valore in centesimi di qualsiasi rapporto, si prende il logaritmo in base 2 di quel rapporto e lo si moltiplica per 1200, cioè con 100 e poi con 12. Il nome “cent” non deriva dalla moltiplicazione con 100, che sposta le due cifre decimali a destra; proviene dai 100esimo parte di un “semitono” altrettanto temperato. 12 è il numero di toni in temperamento uguale, quindi avere questo numero come riferimento per esprimere altre accordature è arbitrario. Un’unità di misura concepita per una sola scala non può rappresentarne adeguatamente altre.
Un’altra unità logaritmica nota come “savart” porta il logaritmo alla base 10 dei rapporti musicali e lo moltiplica per 1000 per comodità. Questo numero non implica un’accordatura a 10 toni, ma il 10esimo armonica in un’accordatura pura avrà sempre il valore di 1000 savarts. Sebbene il nostro sistema numerico sia di base 10, e anche se il savart è un’opzione di gran lunga migliore del centesimo, l’uso del logaritmo di base 10 per le misurazioni musicali non è ancora giustificabile.
L’unità di misura degli intervalli musicali che chiamo “costante” si basa sul logaritmo naturale, noto anche come logaritmo alla base e. Questo è molto diverso dalle scelte probabilmente arbitrarie di 2 e 10, perché e è il tasso base di crescita condiviso da tutti i processi in continua crescita.25 Da un punto di vista musicale, la “crescita continua” è la differenza tra suonare un tono dopo l’altro invece di scivolare da un tono all’altro, dove la diapositiva (o scorrimento, sweep, portamento) contiene tutte le informazioni sonore tra i toni.
Il logaritmo naturale non favorisce alcun intervallo musicale, perché e non è un numero razionale che definisce un solo rapporto; non può essere un tono di qualsiasi accordatura armonica. In quanto tali, le costanti non favoriscono alcun sistema di sintonizzazione. Tutte le scale sono trattate allo stesso modo, trasmettendo le differenze di tono attraverso lo stesso uso astratto dei decimali. Questo perché e è un numero trascendentale: una frazione continua infinita che contiene la sequenza di tutti i numeri naturali e la sequenza di tutti gli intervalli musicali.26
Il valore numerico di e rappresenta il punto teorico all’infinito in cui convergerebbe la frazione continua, ed è per questo che questo numero ha decimali infiniti:
e = 2,718281828459045235360287471352662497757…
Il nome “costante” deriva da e, perché, con la possibile eccezione di π, e è la costante più importante in matematica27 e la base del logaritmo naturale. La formula per calcolare la costante di qualsiasi rapporto musicale è prendere il suo logaritmo naturale e moltiplicarlo per 1000, per la comodità di spostare i decimali di tre posizioni a destra. Formula del foglio di calcolo: “=LN(x/y)*1000” (senza virgolette). Per esempio:
ln × 1000 = 405.465 costanti
Lasciando da parte i numeri, il modo migliore per confrontare gli intervalli musicali è visivo. La costante diventa ancora più potente quando viene tracciata su una linea numerica.
“What You See İs How You Hear” Linea di numeri armonici
Ogni segno rappresenta il logaritmo naturale di ogni valore, ma sono i rapporti effettivi (e i numeri armonici) che vengono scritti sul grafico. Questa linea numerica armonica è infatti una linea numerica logaritmica e raffigura accuratamente gli intervalli musicali nel modo in cui li percepiamo attraverso il senso dell’udito. Chiamo questo strumento di misurazione visiva la linea numerica armonica “What You See İs How You Hear”.
Si noti che questo costrutto non rappresenta visivamente le lunghezze delle corde o dei tubi utilizzati per generare quei toni, né le distanze tra i fori del flauto, e non ha alcuna connessione diretta con le divisioni della tastiera degli strumenti a corda, il che significa che non è uno strumento né un modello per calcolare le distanze tra i tasti. È un diagramma astratto, un grafico matematico che riflette il modo in cui percepiamo le frequenze sonore e non ha nulla a che fare con il modo in cui il suono viene generato e propagato attraverso l’aria.
Notazione semplice
Culturalmente, sembra che ci sia stato in qualche modo fatto il lavaggio del cervello nel credere che la musica sia questo insieme limitato di regole e strumenti governati da un temperamento uguale – la più dissonante di tutte le scale! Le nostre orecchie sono state condizionate ad accettare e piacere, ma questo non lo rende migliore. La tastiera del pianoforte in bianco e nero è uno degli strumenti più difficili da imparare e suonare, e la notazione del personale ideata per questo può solo peggiorare le cose. Spesso mi chiedo come questo possa andare in giro inosservato.
La tastiera standard è proprio come avere un veicolo a 4 ruote con tre ruote rotonde e una quadrata, noto a tutti, usato e lodato da tutti, ma senza che la sua praticità ed essenza vengano mai messe in discussione. Potremmo costruire strade in gomma e progettare l’auto con sospensioni regolabili in tempo reale più sedili fluttuanti magneticamente, ma questo non risolve il problema: non cambia l’unica “ruota” quadrata in un cerchio. Allo stesso modo, potremmo costruire sintetizzatori e sviluppare meccanismi di rilevamento espressivo nelle tastiere, ma questo non risolve il problema: non rende regolare il layout irregolare dei tasti.
La notazione del personale di 5 righe è uno dei sistemi più ambigui di lettura e scrittura musicale. Originariamente concepito per adattarsi all’anatomia della tastiera irregolare del pianoforte, è ingombrantemente utilizzato per tutti gli altri strumenti che ovviamente non hanno tasti irregolari in bianco e nero. Ancora più paradossale, l’armonia moderna non ha nulla in comune con la serie armonica. Cerca di approssimarlo, ma non ci va.
La scala di accordatura temperata, la tastiera irregolare, insieme all’ambigua notazione del personale, i nomi delle note e il centesimo come unità di misura sono solo idee, simboli e strumenti usati in passato. Sono semplicemente concetti che non possono definire la vera natura della musica. Ci hanno servito bene finora quindi diciamo solo addio perché ora hanno bisogno di andare dove appartengono: dietro il vetro delle vetrine all’interno dei musei.2
Ringve, Museo Nazionale della Musica della Norvegia28
Sergio Aschero, dottore in musicologia, ha trascorso 35 anni a ideare e perfezionare un sistema di notazione basato su colori, forme geometriche e numeri che è così semplice che i bambini piccoli e i disabili mentali possono usarlo quasi istantaneamente.29
Tenendo presente che la tastiera Terpstra può cambiare il colore di ogni tasto e la nuova tastiera ha tasti colorati, che i colori possono essere posizionati o dipinti sui manici della chitarra e intorno ai fori del flauto, e che un massimo di 7 toni sono generalmente usati in qualsiasi composizione, la notazione “numerofonica” di Aschero (Numerofonía) può essere facilmente utilizzata in combinazione con la scala dei suoni sacri delle armoniche naturali. Questa notazione è ovviamente retrocompatibile e può essere utilizzata con la corrente o qualsiasi altro sistema di sintonizzazione.
La notazione del personale di 5 righe vs. Numerofonía de Aschero (Geometrica e aritmetica)30
Evoluzione musicale
Il 3rd Millennium Musician non può permettersi di perdere tempo nel cercare di capire la notazione controintuitiva, agonizzando per suonare strumenti quasi impossibili, e nemmeno su dilemmi come quale frequenza di riferimento suona meglio in egual temperamento. Finché la scala è ugualmente temperata, qualsiasi intonazione del concerto può portare solo piccoli e insignificanti cambiamenti. Ora, più che mai, abbiamo bisogno di guardare alla musica e alla scienza della frequenza e della vibrazione con un nuovo set di occhi. E ascolta con una nuova serie di orecchie liberate.
“What Music Really İs: The Manual for The 3rd Millennium Musician, Spiritual Seeker and Free Energy Discoverer” sarà il primo libro di storia scritta che descrive la musica per quello che è veramente, e non attraverso le definizioni di un solo sistema musicale culturale utilizzato solo in alcune parti del mondo. Ciò si ottiene con disprezzo per la nomenclatura standardizzata localmente, le convenzioni stabilite e i riferimenti basati sulla storia, e significa che per la prima volta nella storia l’innocente amante della musica non dovrà preoccuparsi di nozioni astratte con riferimenti circolari per comprendere la musica.
Niente più “toni” e “semitoni” (la parola “tono” come viene usata in questo lavoro significa “tono musicale” o “suono con struttura armonica regolare” e non ha nulla a che fare con la definizione datagli dalla teoria musicale occidentale), non più “taglienti” e “piatti”, nessun “terzo”, “quinte” e “ottave”, “maggiore”, “minore”, “aumentato”, “tonico”, “dominante”, “diatonico” e “cromatico” – sono tutti errori dino e impedimenti.
La musica è un linguaggio universale che non può essere definito attraverso concetti locali. Tutto quanto sopra si riferisce strettamente al sistema musicale occidentale che è di per sé limitato e incoerente con la natura, e come tale non ha il potere di trasmettere ciò che la musica è veramente. Eppure ogni studio della musica si basa su questi concetti peculiari. La serie armonica viene scritta come note sul bastone di cinque righe, anche se questa notazione non può rappresentarla correttamente. Ogni volta che la serie armonica viene spiegata con l’aiuto di un pianoforte, la verità viene tralasciata. Non importa ciò che i musicisti addestrati vogliono farci credere, la verità musicale è che la serie armonica non può essere trovata come tale tra i tasti del pianoforte temperato uguale, né sui tasti di chitarre temperate uguali.
Attualmente abbiamo, e abbiamo da molto tempo ormai, tutti gli strumenti necessari per riportare la vera armonia nella musica. Sta a noi essere coscienti e mettere in discussione tutto. Invece di andare ciecamente dietro al sogno di qualcun altro, andiamo per il nostro. Gli strumenti musicali qui presentati: strumenti musicali, nomi di tono, unità di misura e semplice notazione, possono essere utilizzati con la Scala dei Suoni Sacri e anche con tutte le altre scale di accordatura e frequenze di riferimento immaginabili.
La Sacred Sounds Scale armonizza le frequenze 424, 432, 440 e 528 Hz in un unico Tuning avente il tono di riferimento 1/1 su 256 Hz. Questa scala di accordatura proviene dalla Serie Naturale Ascendente di Armoniche da 32 a 64 del Tono Fondamentale a 8 Hz e pone fine ai dilemmi di accordatura e ai problemi di consonanza dei secoli passati.
La “guerra dei diapason” è finita ora. Pace e Armonia.





































Commenti recenti